Data and Routines - The Center of Gravity

The oscillation modes of black holes, called quasinormal modes, are fundamental quantities in gravitational-wave astronomy, no-hair tests of General Relativity and even in a gauge-gravity duality context. Here you can find useful material for research, including comprehensive data for the quasinormal mode spectrum of Kerr black holes, and powerful yet simple routines to compute them. The data and routines are freely available, but we would appreciate if you reference the original work.

RINGDOWN DATA
Description	References	Download
Frequency basis for parametrized black hole QNMs	arXiv:1901.01265 arXiv:1906.05155 arXiv:2001.09613	decoupled data coupled data decoupled quadratic data
Schwarzschild QNMs Format: 2Mω_R, 2Mω_I, error, n	arXiv:0905.2975 arXiv:0309112	s=l=2 dat file s=l=1 dat file s=l=0 dat file
Kerr QNM frequencies (Gravitational s=-2) Format: a/M, Mω_R, Mω_I, Re[A_lm], Im[A_lm] We start counting from n=1	arXiv:0905.2975 arXiv:0512160	l=2 tar file l=3 tar file l=4 tar file l=5 tar file l=6 tar file l=7 tar file
Kerr QNM frequencies (Electromagnetic s=-1) Format: a/M, Mω_R, Mω_I, Re[A_lm], Im[A_lm] We start counting from n=1	arXiv:0905.2975 arXiv:0512160	l=1 tar file l=2 tar file l=3 tar file l=4 tar file l=5 tar file l=6 tar file l=7 tar file
Kerr QNM frequencies (Scalar s=0) Format: a/M, Mω_R, Mω_I, Re[A_lm], Im[A_lm] We start counting from n=1	arXiv:0905.2975 arXiv:0512160	l=0 tar file l=1 tar file l=2 tar file l=3 tar file l=4 tar file l=5 tar file l=6 tar file l=7 tar file
KN QNM frequencies (Gravitational modes) Format: a/M=Q/M, Mw_R,Mw_I (fundamental mode)	arXiv:1501.04625	dat file
QNM Excitation factors (scalar, vectors and tensors) Format: a/M, Mω_R, Mω_I, Re[A_lm], Im[A_lm]; Re[B_Teuk]; Im[B_Teuk];Re[B_SN]; Im[B_SN];	arXiv:0605118 arXiv:1305.4306	s=2 tar file s=1 tar file s=0 tar file
Fits to Kerr QNMs Format: l, m, n, f₁, f₂, f₃, q₁, q₂, q₃ Mω_R=f₁+f₂(1-a/M)f₃ Q=q_¹+q₂(1-a/M)q₃	arXiv:0905.2975 arXiv:0512160	dat file
QNM frequencies with 20-digit precision by Plamen Fiziev.	arXiv:1109.1532	zip files
Kerr QNM frequencies and excitation factors (scalar, electromagnetic, gravitational) Format: a/M, Mω_R, Mω_I, Re[A_lmn], Im[A_lmn], Re[M^(-2s) B_Teuk], Im[M^(-2s) B_Teuk], Re[B_SN], Im[B_SN]	arXiv:2504.00084	s-2 s-1 s0 s1 s2

RINGDOWN ROUTINES
Description	References	Download
Computation of Kerr QNMs with Leaver’s method	arXiv:0905.2975 arXiv:0512160	Notebook
Computation of Regge - Wheeler and Zerilli equation using Mathematica and xTensor	Regge & Wheeler, Phys. Rev. 108, 1063 (1957) Zerilli. PRL24, 737 (1970)	Notebook
Computation of QNMs with direct integration	arXiv:1004.4007	Notebook
Python code to perform bayesian inference based on parallelized nested sampling on numerical relativity or perturbation theory waveforms.	arXiv:2308.14796	bayRing.zip
Julia code to evolve axial gravitational perturbations to the Vaidya spacetime, as well as to perform bayesian inference using a ringdown model which incorporates nonlinear effects in the background.	arXiv: 2312.04633	Vaidya-PT.zip
Set of Mathematica and Julia routines accompanying 2502.18643, including linear perturbations of spherically symmetric spacetimes with stable trapping.	arXiv: 2502.18643	StableLR
Mathematica routines to perform perturbation theory on spherically symmetric backgrounds, exploiting the 2+2 split of Einstein's equations, including the linearized equations of self-gravitating fluids in the BDNK theory of hydrodynamics.	arXiv:2411.16841	PertBDNKStars
Computation of SAdS QNMs using power-series methods	arXiv:0905.2975 arXiv:0105103	Notebook
QNMs of RNdS black holes	arXiv:1709.09178 arXiv:1711.10502	Notebook
Proca fields on a Kerr BH slow-rotation approximation	arXiv:1209.0465 arXiv:1209.0773	Notebook Coefficients.mx
QNMs of Kerr-Newman BHs slow-rotation approximation	arXiv:1304.1160	Notebook
Massive spin-2 fluctuations slow-rotation approximation	arXiv:1304.6725	Notebook
Solves the eigenspectrum of unstable modes of a Kerr BHunder massive scalar perturbations through Leaver's continued fraction method	arXiv:1501.06570	Notebook
Computation of the QNMs of EDGB black hole	arXiv:1609.01286	Notebook

Superradiant Bounds on Ultralight Fields

See Brito, Cardoso and Pani, Superradiance, Lectures Notes in Physics 906 (2020).

SUPERRADIANT BOUNDS ON ULTRALIGHT FIELDS
Excluded Region (in eV)	Source	References
5.2x10^-13 < m_S <6.5x10^-12 * 1.1x10^-13 < m_V <8.2x10^-12 * 2.9x10^-13 < m_T <9.8x10^-12 *	Direct bounds from absence of spin in Cyg X-1	arXiv:1801.01420 arXiv:2002.04055
3.8×10⁻¹⁴ < m_S < 2x3.4×10⁻¹¹ 5.5×10⁻²⁰ < m_S < 1.3×10⁻¹⁶ 2.5×10⁻²¹ < m_S < 1.2×10⁻²⁰ 6.2×10⁻¹⁵ < m_V < 3.9×10⁻¹¹ 2.8×10⁻²² < m_V < 1.9×10⁻¹⁶ 2.2×10⁻¹⁴ < m_T < 2.8 ×10⁻¹¹ 1.8×10⁻²⁰ < m_T < 1.8×10⁻¹⁷ 6.4×10⁻²²< m_T < 7.7×10⁻²¹	Indirect bounds from BH mass-spin measurements	arXiv:1411.2263 arXiv:1209.0465 arXiv:1304.6725 arXiv:1704.05081 arXiv:1706.06311 arXiv:1805.02016 arXiv:1801.01420 arXiv:2002.04055 arXiv:2009.07206 arXiv:2012.12790
1.2×10⁻¹³ < m_S < 1.8×10⁻¹³ 2.0 ×10⁻¹³ < m_S < 2.5 ×10⁻¹² m_V: NA m_T: NA	Null results from blind all-sky searches for continuous GW signals	arXiv:1909.08854 arXiv:2003.03359
6.4×10⁻¹³ < m_S < 8.0×10⁻¹³ m_V: NA m_T: NA	Null results from searches for continuous GW signals from Cygnus X-1	arXiv:1909.11267 arXiv:1407.2030
2.0×10⁻¹³ < m_S < 3.8×10⁻¹³ 0.8×10⁻¹³ eV < m_V<6.0×10⁻¹³ eV m_T: NA	Negative searches for a GW background	arXiv:1706.05097 arXiv:1706.06311 arXiv:2011.06995
5×10⁻¹³ < m_S < 3×10⁻¹² m_V ~ 10⁻¹² m_T: NA	Bounds from pulsar timing	arXiv:1704.06151 arXiv:1908.10440
2.9×10⁻²¹ < m_S < 4.6×10⁻²¹ 8.5×10⁻²² < m_V <4.6×10⁻²¹ 7.2 ×10⁻²² < m_T < 2.5 ×10⁻²⁰	Bounds from mass and spin measurement of M87 with EHT	arXiv:1904.09242 arXiv:2009.07206

* See Brito, Cardoso and Pani, Superradiance, Lectures Notes in Physics 906 (2020).

Amplification Factors in Kerr and Routines

Superradiant amplification of massless waves scattering off Kerr black holes is an important phenomena in curved spacetime. Details of the process can be found in an outstanding work by Press and Teukolsky (ApJ193, 443 (1974)), but extensive tables and routines to compute them are lacking. We provide here such data. The routines are freely available, but we would appreciate if you refer to the original work.

AMPLIFICATION FACTORS DATA AND ROUTINES
Amplification Factors Data	References	Download
Amplification factors of massless fields in the Kerr background.	arXiv:1501.06570	Data
Amplification Factors Routines	References	Download
Amplification factors of the superradiant scattering of a charged wave off a spherically-symmetric or a slowly-rotating BH with generic metric.	arXiv:1501.06570	Notebook
Amplification factors of the superradiant scattering of a neutral bosonic wave of generic spin off a Kerr BH, obtained by solving the Teukolsky equations.	arXiv:1501.06570	Notebook

Gravitational Waves from Viscous Stars

GRAVITATIONAL WAVES FROM VISCOUS STARS
Description	References	Download
Notebook handling axial-led fluctuations of a slowly rotating star in the BDNK hydrodynamic theory. Requires RGtensors package.	arXiv:2411.16861	rotating_stars.nb
Julia routines to integrate stellar structure equations and axial perturbation equations derived in the previous notebook, and to extract reflectivities.	arXiv:2411.16841	jl_rotating_stars.zip

Cardoso et al. Metric functions and perturbations equations for black hole solutions in Effective Field Theories. Phys. Rev. Lett. 121: 251105 (2018). [arxiv:1808.08962]

Readme (Rich Text Format)
Effective Potencials Webpage (Mathematica Notebook)
EFT BH Geodesics (Mathematica Code)
EFT BH Metric (Mathematica Code)

Solutions of Einstein's equations can be obtained analytically in a handful of cases. Generically, it requires sophisticated techniques. Here we show some simple routines (under the form of notebooks or C++ routines) to compute (stationary) hairy black hole solutions in massive theories of gravity and static neutron star structure in alternative theories of gravity. Finally, we also make available a 1+1 code to evolve a spherically symmetric, scalar wavepacket in AdS spacetimes. The routines are freely available, but we would appreciate if you reference the original work.

NONLINEAR SOLUTIONS
Description	References	Download
Rotating black holes in galactic haloes	P. G. S. Fernandes and V. Cardoso, to appear (2025)	Routine
Hairy BHs in massive gravity	arXiv:1309.0818	Notebook 1 Notebook 2
NSs in scalar-tensor gravity Slow-rotation approximation	arXiv:1405.4547	Notebook
Scalar Field Collapse in AdS	Lopes et al. [MSc Thesis]	Notebook/Routines
Kerr black holes with scalar hair	arXiv:1403.2757	Data
(i) computes and solves Einstein's equations for a rotating self-gravitating perfect-fluid to second order in the spin. (ii) derives in detail the procedure to separate the Klein-Gordon equation in this background.	arXiv:1501.06570	Notebook

Boson Stars
Description	References	Download
Spherically symmetric boson stars (scalar, vector and charged).	arXiv:1302.2646 arXiv:1307.4812	int_bs

Tidal Love numbers for exotic compact objects (boson stars, gravastars, wormholes, mirrors).

TIDAL LOVE NUMBERS
Description	References	Download
Love numbers of ECOs.	arXiv: 1701.01116	ECO Dat Files TLNs.nb
Basis for parametrized black hole TLNs.	arXiv: 2310.19705	Basis.zip

Radiation from Plunging Particles

Gravitational radiation from point-like particles plunging into black holes has a very long history, and is known to reproduce accurately even highly non-linear processes like equal mass black hole collisions. We will gather here some Mathematica routines to compute gravitational radiation from the plunging of particle into black holes, both in GR and in some modified theories of gravity.

RADIATION FROM PLUNGING PARTICLES
Description	References	Download
Radiation from a pointlike particle plunging into a Reissner-Nordstrom black hole.	arXiv:1604.07845	Notebook
Radiation from a pointlike particle plunging into a EDGB black hole.	arXiv:1609.01286	Notebook
Perturbation of Schwarzschild black hole in dRGT massive gravity.	arXiv:1809.00673 arXiv:2304.01252	Notebook

Gravitational Waves from Boson Clouds

Here you can find routines that can be used to compute the flux in gravitational waves emitted by a scalar cloud around a Kerr black hole. Some computations make use of the Black Hole Perturbation toolkit (bhptoolkit.org). We also use results from arXiv:0306120, arXiv:0705.2880 and arXiv:1312.2326. The data generated by this routine served as input for the python package gwaxion (pypi.org/project/gwaxion).

GRAVITATIONAL WAVES FROM BOSON CLOUDS
Description	References	Download
Computation of gravitational-wave flux from a scalar cloud.	arXiv:1706.06311 arXiv:1706.05097	Notebook
Scalar and gravitational fluxes from EMRIs in scalar environments.	arXiv:2312.06767	File

EMRIs in Astrophysical Environments

Here you can find routines to compute the radiation emitted by an extreme-mass-ratio inspiral in spherically-symmetric, non-vacuum black-hole spacetimes. We specialize to the case of a black hole within a halo of matter based on the solution found in arXiv:2109.00005, but you can adapt it to other backgrounds.

EMRIs in Astrophysical Environments
Description	References	Download
Time-domain code	arXiv:1108.1816 arXiv:2210.01133	Polar_HALO.c Axial_HALO.c
Frequency-domain code	arXiv:1604.07845 arXiv:2210.01133	EMRI_environment.zip

Video Files

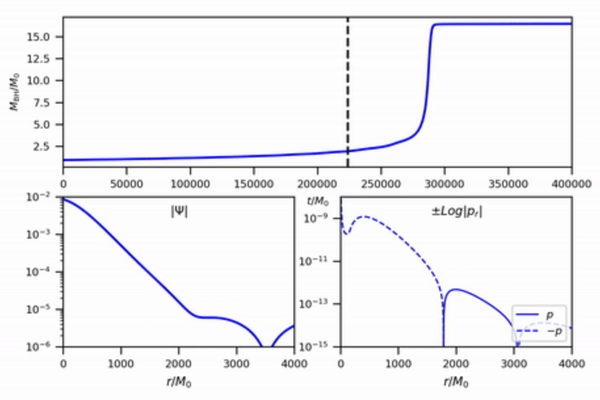
Parasitic black holes. The swallowing of a fuzzy dark matter soliton. Time evolution of BH mass (top panel), scalar field (bottom left), and energy flux (bottom right). Initial boson star mass is 15 times heavier than initial black hole mass. Initial boson star size is 600 times larger than black hole radius. arXiv:2207.09469v1.

Piercing of boson stars by a black hole-1

Piercing of boson stars by a black hole (I). A black hole of unit mass colliding with a boson star of mass 0.53. The collision happens at 50% the speed of light. arXiv:2206.00021.

Piercing of boson stars by a black hole-2

Piercing of boson stars by a black hole (II). A black hole of unit mass colliding with a boson star of mass 0.53. The collision happens at 50% the speed of light. Right panel: a black hole of mass 0.1 colliding with a boson star of mass 0.53. The collision happens at 50% the speed of light. arXiv:2206.00021.

High energy black hole collisions. The collision of two boosted black holes (v=0.75c in the center of mass frame), with a finite impact parameter in asymptotically flat spacetime. About 24% of the center of mass frame can be released as radiation, for this collision. The final hole is nearly maximally spinning. The intensity of the color refers to the amplitude of the gravitational waves as measured by Ψ₄. arXiv:0907.1252.

Black holes in a box. The inspiral and coalescence of two black holes, with total mass M, inside a confining box of radius 48 M. Out- and in-going waves are measured respectively by Ψ₄ and Ψ₀. arXiv:1004.4633.

Black hole bombs I: Scalar fields. The time evolution of a massive scalar field around a highly spinning black holes. The scalar field is initially in a bound state, and continues to be for thousands of orbital periods. Colors depict field intensity. arXiv:1212.0551.

Black hole bombs II: Vector fields. The time evolution of a massive vector field around a highly spinning black holes. The vector field is initially a generic gaussian. Colors depict field intensity. arXiv:1212.0551.

Black hole collisions in de Sitter spacetime. Two black holes of sufficiently large mass in de Sitter spacetime would, upon merger, give rise to too large a black hole to fit in its cosmological horizon, resulting in a naked singularity. We here test such a configuration. Even though the initial separation is very small, we find that the holes move away from each other, with a proper separation increasing as the simulation progresses. arXiv:1204.2019.

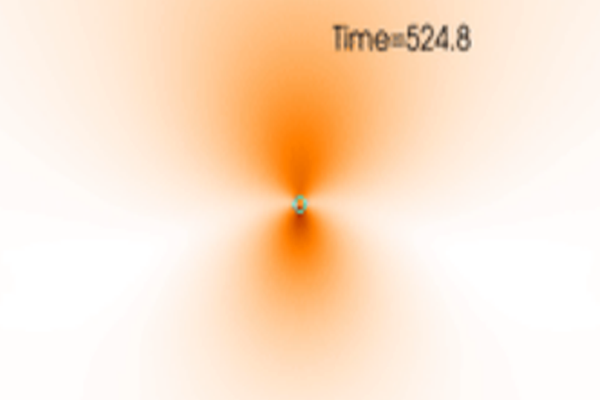
Bursts of light from axion clouds (I). The evolution of an axion Phi of mass mu=0.2 and of the electromagnetic scalar E²-B² in the background of a Kerr BH (a=0.5). The initial axion configuration describes a cloud around a spinning black hole, grown by superradiance.

When superradiance is turned off and the initial amplitude of the axion is small, any vector perturbation dies off quickly. arXiv:1811.04950.

Bursts of light from axion clouds (II). When superradiance is turned off and the initial amplitude of the axion is large, an instability is triggered and gives rise to a EM burst. arXiv:1811.04950.

Bursts of light from axion clouds (III). When superradiant growth is included, even a small initial axion amplitude eventually grows large and triggers EM bursts, blasts of laser-like electromagnetic radiation. This blasts lowers the axion to sub-critical values, until superradiance dominates again. arXiv:1811.04950.

Turbulent accretion disk around a supermassive black hole-1

Turbulent accretion disk around a supermassive black hole (I). The turbulent gas flow stochastically excites the quasinormal modes of the central black hole which leads to gravitational wave emission.

Turbulent accretion disk around a supermassive black hole-2

Turbulent accretion disk around a supermassive black hole (II). See description above.

Audio Files

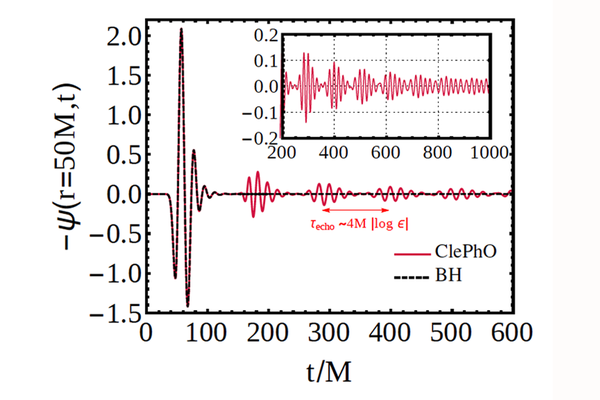
Echoes from quasicircular inspiral of a mass ratio 1:100 binary. Massive object is a ClePhO (horizonless object). arXiv:1602.07309; arXiv:1608.08637; arXiv:1904.05363.

Audio data:
audio q=[1 .. 100] quasi-circular echoes;
wave 22, Schwarzschild Radius 100

Black Hole Spectroscopy

Superradiance

Black Hole Solutions in Effective Field Theories

Nonlinear Solutions and Boson Stars

Tidal Love Numbers

Gravitational Radiation

Video and Audio Data